|
 もくじ
もくじ
機関車の誕生
試行錯誤
機関車の限界
機関車の終焉
 機関車の誕生
機関車の誕生

リチャード・トレビシック(1771〜1833)
機関車というのは蒸気機関車であれ、電気機関車であれ、ある種のイメージを持っている。
客車や長い貨物列車を牽引している姿も良いが、任務を解かれて機関庫や側線で独り佇む姿も良い。
鉄道写真の被写体としても機関車は華があるし、単なる機械というものを越えたどこか人間臭さ、人格のようなものを感じることがある。
英国の機関車トーマスというTV番組を見れば判るように、擬人化された機関車は人気の的である。
ウィキペディアによると、”リチャード・トレビシックが初めての蒸気機関車を制作したのが1802年。その特許を買ったサミュエル・ホンフレイはトレビシックの蒸気機関車が10トンの鉄を牽引して、とある区間(約16km)を運べるか賭けを行い、1804年2月21日、ペナダレン号と命名された機関車が10トンの鉄と5両の客車、それに乗った70人の乗客を4時間5分で輸送することに成功した。” とされている。
この時、16Kmを4時間5分を掛けて輸送しているのだから、平均時速は3.9Km/hということになり、人が歩く速さだったことになる。最初の試みであるから、ホンフレイやトレビシックらはハラハラしながらそれを見守っていたであろう。もし当時テレビがあったなら実況中継をしていたかもしれない。
このときの機関車の重量は5トンと言われている。この機関車で10トンの鉄と5両の客車、それに乗った70人の乗客であるから、仮に鉄を載せる貨車を10トン、当時の客車を1両あたり5トン、人間の体重を60Kgとすると、貨車+客車の重量が10+5×5=35トン、運びたい鉄と乗客の重量が10+0.06×70=14.2トンであるから、総重量35+14.2=49.2トンの貨客車を自重5トンの機関車が平均時速3.9Km/hで牽引した訳である。
この価値を想像するために、同じ重量の荷物を私達に馴染みのある現代の輸送手段で運ぶことを考えると、およそディーゼル内燃機関を積んだ大型トレーラーを使うのが一般的であろう。(但し日本の法規上、公道を通行できるのは総重量25トンまでで、それを越える重量物を運ぶには所定の手続きが必要である)
このクラスのトレーラなら49.2トンの荷物を積んで、時速は60Km/hで走行可能であろう。但し、これは平坦な場合であり、平らな土地と言っても16Kmの区間には少なからず傾斜=10‰(1000m進んで10m上がる)〜20‰の勾配があるのが普通なので、例えば10‰の勾配にさしかかるだけで速度は30Km/h程度まで落ちてしまうものである。
それでも、平均時速にして30Km/h程度では運べるであろう。およそ200年でその価値はざっと8倍と言ったところだろうか。
しかしながらどんな革新的なシステムでも始まりはこのようなものだったのだろう。競合するようなライバルは居なかったので、走り出したビジネスは転がり続けるしかなかったようである。
さて、もう少し当時の様子を想像してみよう。
前述の ”とある区間” は、恐らく地理的になるべく平坦な区間が選ばれたであろうことは想像に難く無い。ビジネスチャンスか否かと見守る投資家達に訴求するには、途中で止まってしまうことは避けねばなるまい。ペナダレン号がどの程度の性能を持っていたのかは計測されていないが、大きさから推測すると恐らく10‰の勾配があれば途中で止まってしまうレベルではないかと思われる。
であるから、4時間5分のドラマの中身は、登り坂では止まりそうになったペナダレン号を後ろから押してやろうという見物人が出て来たかもしれないし、下り坂ではいっしょに走り出す者も見られたのではないだろうか?
坂で止まったかどうかは定かではないが、止まった事実はあったにしても、記録としてはあえて書かなかったり、書かれたものは始末されたかもしれない。
もくじへ戻る
 試行錯誤
試行錯誤
このイベントにおける成果をトレビシックは技師としてどう見ていたのだろうか?
蒸気機関による鉄道の有用性が認められ、蒸気機関車の設計がルーチンワークとなるまでにはその後、50年ほど掛っていると思われる。
アメリカの南北戦争(1861〜1865)では当時、蒸気船や蒸気機関車による物資の輸送が重要な鍵を握っており、より重い荷物を速く運ぶために機関車はどんどん大型化している。
機関車による物流が軌道に乗ると逆に、ある都市間で一日当り○○○○トンの貨客を運びたい。その途中には最大△%の勾配を持った峠を越えなければならない。
最悪事態を想定し、○○○トンの列車が峠で停車を余儀なくされ、再度引っぱり出すにはどの程度の牽引力、大きさの機関車が必要なのか?という計算が始まる。
例えば、トラ級の貨車が自重約9トン、荷重17トンクラスなので、総重量は26トン。これが40両連なれば、26×40=1040トンというオーダーになる。
トレビシックやホンフレーの時代は機関車というシーズ=seedsが先にあったが、今度はニーズ=needsが先になるということである。
その計算は高校の数学や物理で習うレベルの知識だけで可能なのだが、実際にはそうは簡単に問屋は卸してくれなかったようである。
人間が荷物を背負って斜面を登ってみればすぐ判る。滑り難く、靴が斜面をしっかりグリップしていれば足に力を込めれば前進は可能である。ところが雨でぬかるんでいたり、凍結でもしていようものなら足にいくら力を込めても滑ってしまい、前進することは適わない。
やっかいなのはこのグリップ=摩擦力のことで、氷上のように摩擦力が小さければ重いそりを引こうとむやみに氷を蹴っても滑って前に進めない。
鉄道の場合、鉄製のレールと車輪の間が雨で濡れているときの摩擦力は機関車の自重のおよそ1/10である。それしか受け止められないのである。このとき、摩擦係数=1/10=0.1と言う。
図1
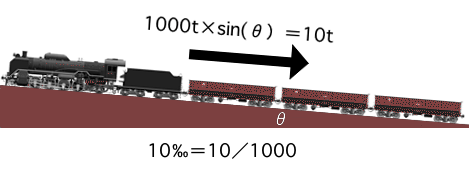
図1を見て頂きたい。 仮に10‰勾配の坂で、進行方向とは反対にずり落ちようとする総重量1000トンの貨客車を止めておくには1000×sin(θ=10‰勾配に相当する傾き角)=9.9995トン=ほぼ10トンの牽引力が必要になる。これ以上の力を掛けないと機関車と貨客車はそこに止まっていることは出来ても動き出せないのである。
仮に11トンの牽引力が発揮できる機関車であっても、その自重が100トンであればその1/10の10トンの摩擦力しか無い=伝えられないという事である。
実際には車輪上では11トンの牽引力が働くのであるが、10トンを越えたところで残りの1トンは車輪を空転させて熱に変ってしまうのである。
その状態を続けていれば車輪とレールの間で煙が上がる筈である。つまり、悪戦苦闘しつつ、ずり下がるのを止めるだけで精一杯なのである。
こんなところが機関車が人間味を感じさせる所以かもしれない。
平坦な区間で1000トンの貨客車を楽に牽引できても、雨降る峠で20‰の勾配に差し掛かると車輪は空転を始め、スピードが落ちてついには止まってしまう。そして次の瞬間にはブレーキを掛けていたとしても車輪はロックしたまま進行方向とは逆にずり落ち始めるという、とても想像したくない事態に陥ってしまうのである。
恐らく、トレビシックやホンフレイの時代はやってみて判ったのではないかと思われる。産業革命は驀進しても理論が追いついていなかった時代である。
冒頭で、サミュエル・ホンフレイはトレビシックの蒸気機関車が10トンの鉄を牽引して、とある区間(約16km)を運べるか賭けを行ったことを紹介したが、賭けの意味は二つ考えられそうである。
ひとつは、何回かの試運転で、雨の日は緩い坂でも車輪がスリップして登れなくなることを経験していたので、当日の天気に賭けていた。
もうひとつは、雨だった場合を想定して、試運転を繰り返して総重量を登れるだけの範囲に抑えていた。すなわち勝つと確信した賭けであったということである。
最初は10トンの鉄板を牽引出来るか?というものであったが、実際には5両の客車、それに乗った70人の乗客をプラスしても牽引できたところを見ると、この賭けは後者だったのではないだろうか?
もくじへ戻る
 機関車の限界
機関車の限界
この試行錯誤の過程で先人は車輪の空転を防ぐ策を考えた。
空転を始めたら砂を撒く。摩擦力を補うということである。しかし、空転の頻度が高ければ砂箱はいずれ空になるし、レールと車輪も摩耗する。
もうひとつの策は、原理的に摩擦力は物体の重量×摩擦係数である。
すなわち、機関車の自重を10%増やせば伝えられる牽引力も10%増える計算になる。
先述の雨降る10‰勾配の坂で伝え切れなかった1トンの牽引力を有効に使うには、摩擦係数=0.1なら、機関車の自重を1/0.1=10トン増やして110トンにすればよいという事である。
この事は車輪をレールに押し付ける力が10トン増えるということである。雪の坂道で空荷のトラックでは後輪が滑っても、荷物を積めば車輪がグリップして登れるという理屈と同じである。
さて、こんな疑問は涌かないだろうか?
氷上で重いそりを引っ張ろうとする時、自分の背中に荷物を背負っている時とそうでない時で、どちらが速く引っ張り出せるのだろうか?
図2
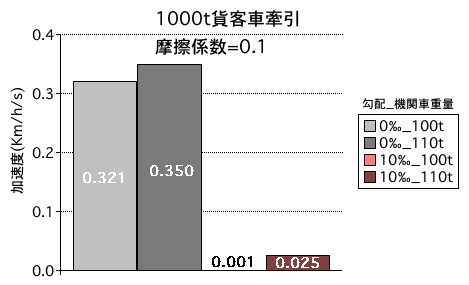
図2を見て頂きたい。雨天を想定して摩擦係数を0.1とした場合、1000トンの貨客車を自重100トンと110トンの機関車で牽引する場合に得られる加速度の違いを示してみた。1秒間に何Km/hずつ速くなるかという数字である。0.3Km/h/sとは3Km/h速くなるのに10秒間掛るという具合である。
これを見ると機関車の自重が10トン重い方が加速度は大きいのである。
これは車輪のグリップ力が増えた=伝えられる牽引力が10%増えたのに対し、機関車と貨客車の総重量に対しては1%しか増えていないからである。機関車のこの10%の重さを死重=dead weightと呼ぶことがある。
しかしながら、走り出して加速し、制限速度で巡航していてもいつかは制動しなければならない。このとき、重いほど列車は止まり難い事は想像できるであろう。ブレーキシューもその分摩耗が進むという事である。死重というのは、”肉を切らせて骨を切る” のと同じかもしれない。
図2でもうひとつ判るのは、勾配0‰の平坦に比べ、10‰の勾配では加速度は1/10以下に落ちてしまうのである。
0.001Km/h/sというと、1Km/h速くなるのに1000秒間掛るということであるから、ナメクジに追い越されるかもしれない。
図3
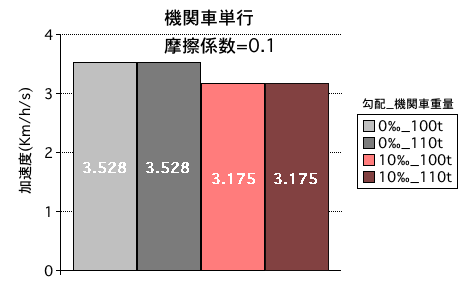
次に図3を見て頂きたい。今度は機関車単行の場合である。
これを見ると、摩擦係数=0.1という制約があれば、機関車の自重が増えても加速度は変わらないという事である。
これは、車輪のグリップ力が増えた分と自重が増えた分が相殺されてしまうからである。
”物体に力が働いた時に、物体の重さに反比例した加速度で動き出す” と言ったのはニュートンであるが、それは地上で物を運ぶのではなく、宙に浮いている状態での話で、摩擦力など考えていないのである。
地上で目の前の機関車と貨客車を動かさねばならないトレビシックにとって、ニュートンはただの気楽な男に思えたかもしれない。高校の物理の教科書とはかように気楽なものなのである。
図2と3を見て判るのは、
・機関車は貨客車を牽引するには自重は必要に応じて重く無ければならない。
・機関車は何も牽引しないなら加速度の上限は摩擦係数で決まってしまい、自重には無関係である。
という事である。
もし機関車トーマスが何も牽引せずに単行で走り回っていれば、トップハム・ハット卿からクビにされてしまうであろう。しかし、新聞や郵便の束を抱えて配達していたら褒められたかもしれない。
さて、次に機関車や貨客車の重量を支えるレールの立場になってみよう。
総重量1000トン級の列車が微小な、例えば1cmの区間を通過する場合、まず100トンの機関車に踏みつけられ、その直後にはトラ級の総重量26トンの貨車が40回踏みつけてゆくのであるから、骨が折れるということである。
鉄は人間と違ってすぐに骨折はしないが、時間を掛けて疲労骨折に至る=機関車の重量が増えればそれに応じて寿命が縮まるという具合である。
これに応えるには太いレールにすれば良い。
しかしながら、枕木を介しているとは言え、それを支える地盤が柔らかければ枕木もろとも陥没してしまう。
このように風が吹くと桶屋が儲かる式に、先人はより重い貨客を輸送しようとすると地面が陥没するという素直な現実に直面したのである。
ある都市間で一日当り○○○○トンの貨客を運びたい。その途中には最大△%の勾配を持った峠を越えなければならない、というニーズに応える場合、それに見合った盤石な地盤と分厚い道床が必要になるという事である。この素直な現実は蒸気機関車が電気機関車になっても変わらないのである。
ところで、今度は荷主や乗客の立場になってみよう。
荷主や乗客は自分を含め、必要な重さの荷物をより速く目的地に届けたいわけだが、何時間ならリーズナブルな運賃と思えるだろうか?
列車は出発したら出来るだけ止まりたくないものだが。途中では給水、給炭、行き先別に貨車を組み替えたりするのでノンストップと言う訳にはいかない。
これが旅客列車で各駅停車ともなれば、加速の遅さが後続の全列車に影響を与えてしまうことになる。
ここで、前述の16Kmを4時間5分掛った価値に戻るわけである。
より重い貨客をより速く運ぶために必要なものは、
・レールと車輪の間の摩擦力の範囲内で輸送トン数に見合った牽引力の確保。
・列車の重量を支える盤石な地盤、頑丈な鉄橋。
と言うことになろうか。
ホンフレイは賭けに勝った後には、こうした試算に迫られたのではないだろうか?
あるいは、”僕は金勘定は苦手だから、助手君、頼むよ!”
今も昔もビジネスとはこういうものかもしれない。
アメリカでどんどん機関車が大型化、高出力化していった背景には、運びたい荷物が右肩上がりに増えていった事情があったのであろう。資源の豊かな国ゆえ、レールも太く重くなればその分、重厚な道床、頑丈な鉄橋を用意するのに迷いはなかったのかもしれない。
資源に乏しく、地盤も盤石とは言えず、険しい山谷の多い島国の日本で頭を悩ませた鉄道技師が居た。
島 安次郎(1870〜1946)である。彼は戦前に、スピードを上げる為にレール幅を世界標準並みに広くする広軌論を唱えた人物である。
そして、その息子、島 秀雄(1901〜1998)は、重い列車を1台ないし重連の機関車が牽引する方式の限界を認め、今日の電車のように動力を分散した方が良いと考えていた人物である。
大きな機関車に重い貨客車を牽引させるのではなく、機関車トーマスのように小さな身体に貨客を載せて連結するという発想である。
もしかしたら、彼は子供の頃にこんな光景を眼にしたのかもしれない。
カブト虫に紐を巻いた石を引っ張らせて遊んでいたが、より大きな石を引っ張らせようとすると六本の足は懸命に地面を蹴るのだが滑って前進できなくなってしまった。目を移すと蟻が行列を成して餌を運んでいる。蟻一匹が運んでいる重さは僅かだが、永遠と連なっている全体を足したら結構な重さになりそうである。

島 安次郎(1870〜1946)
|

島 秀雄(1901〜1998)
|
もくじへ戻る
 機関車の終焉
機関車の終焉
現代、機関車が牽引する貨物輸送は殆ど自動車に取って替わられてしまった。
いろいろな理由が挙げられるのだが、摩擦力という観点から見ると、自動車のゴムタイヤと雨に濡れたアスファルト路面の間の摩擦係数はおよそ0.6程度である。鉄道の鉄製レールと車輪の0.1に対し6倍の摩擦力で牽引力を伝えられるのである。
従って、一般公道を走るトラックやトレーラは100‰の坂をいとも容易く通過してしまうのである。重い荷物を積んで速度が遅いトラックが居れば追い越すこともできる。鉄道では先行する1列車が立ち往生したら全滅である。
このように自動車の圧勝のように見えるが、自動車にも弱点がある。
ゴムタイヤの大きな摩擦力の代償は転がり難いという性質である。街行く自動車のタイヤを見れば直ぐ判る。鉄道のレールと車輪が点で接触しているのに対し、路面とタイヤが接地している部分は目で見てわかるほどの面である。これはゴムタイヤが撓むからであって、撓む事は牽引力の一部分を浪費するのである。その比率は鉄製車輪のおよそ10倍である。
もしトレビシックの時代にゴムタイヤがあったとして、蒸気機関車に履かせてみたら、今度は燃料費が嵩む事に気が付いたかもしれない。
現代では燃料を燃やして出てくる二酸化炭素が人類の生存を脅かしている事を、トレビシックは想像もしていなかったであろう、
あちらを立てればこちらが立たず。しかしながら自動車が有利か鉄道が有利か、目的や用途に応じて試算してみれば、あるいは鉄道による貨物輸送の復権はあるかもしれない。
昭和30年代頃までは、電車や客車には荷物車が連結されていたり、荷物室というものが付いていたものである。近い将来、例えば宅配便のユニフォームを着たお兄さん達が荷物車や荷物室を出入りする姿が珍しく無くなるのかもしれない。
あるいは駅のコンビニで集荷し、希望するお客さんに一品だけ持参してもらい、降りる駅のコンビニで置いていってもらうと機関車トーマスのシールが貰えるとか....
もくじへ戻る
 参考文献
参考文献
物理 高等学校理科用 数研出版刊
|